Back to my home page.
Algorithms on continued and multicontinued fractions
Frank Nielsen
 Abstract:
Abstract:
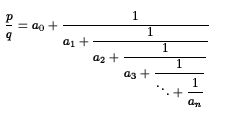
We introduce a continued fraction binary representation of the rationals, and several associated algorithms
for computing certain functions on rationals exactly. This work follows the path
taken by previous works done in that area and extends the notion of continued fraction to
multicontinued fraction.
For that purpose, we introduce the notion of generalized matrix. This work is composed of six parts. We begin
by a survey on the different kinds of representation of numbers. We then describe an algorithm which compute
(ax+b)/(cx+d) for any x when both inputs and outputs are provided piecewise. We generalize this algorithm to compute
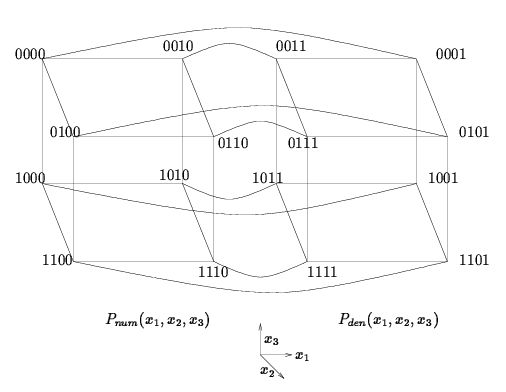
complex functions f(x1, ..., xn)=(P1(x1, ..., xn))/(P2(x1, ..., xn)) where P1(.) and P2(.) are
polynomial functions of n variables. In the remaining, we show it is possible to mix various formats of numbers (both for the input and
output of numbers). Approximation of a real to a rational vector is investigated (Szekeres'algorithm). A matrix representation of
multicontinued fractions is introduced and we develop an algorithm based on that representation to compute quotient of polynomial functions.
Download the PS paper © Frank Nielsen (927 KB size, 73 pages, 19 figures).
Bibtex entry:
@MastersThesis{n-acmd-1993,
author = {Frank Nielsen},
title = {{Algorithms on Continued and Multi-continued fractions}},
school = {Ecole Normale Superieure Lyon},
address = {Lyon, France},
year = {1993}
}
Related publications:
Frank Nielsen,
Algorithms on Continued and Multi-continued fractions,
Rapport de Magistere (Master Science), Ecole Normale Superieure de Lyon, France,
1993.
© Copyright notice.
Last updated, 2003.


