Paper: Maintenance of a Piercing Set/Shooter Location Problem

Maintenance of a Piercing Set/Shooter Location Problem

Matthew J. Katz, Frank Nielsen and Michael Segal

Abstract:
We show how to efficiently maintain a minimum piercing set for a set S of intervals on the line, under insertions and deletions to/from S. A linear-size dynamic data-structure is presented, which enables us to compute a new minimum piercing set following an insertion or deletion in time O(c(S)log|S|), where c(S) is the size of the minimum piercing set. We also show how to maintain a piercing set for S of size at most (1+ε)c(S), for 0 < ε ≤ 1, in O(log|S|/ε) amortized time per update. 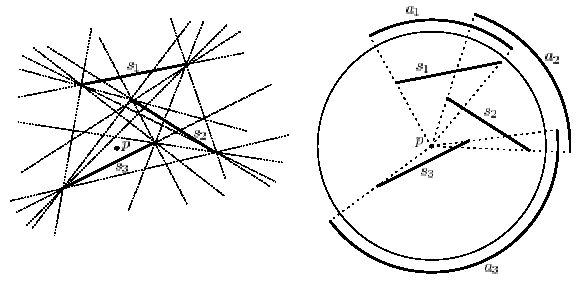We then apply these results to obtain efficient solutions to the following three problems:

the shooter location problem,
computing a minimum piercing set of arcs on a circle,
dynamically maintaining a box cover for a d-dimensional point set.

Key words: geometric optimization, piercing set, dynamic algorithms.

Download the PDF paper here (301 Kb size, 15 pages, 3 figures).

The original publication is available at Springer Link.

doi: 10.1007/s00453-002-1006-1

Bibtex entry:


@Article{kns-mpsia:2003,
  title = {{Maintenance of a Piercing Set for Intervals with Applications}},
  author = {Matthew J. Katz and Frank Nielsen and Michael Segal},
  journal = {Algorithmica},
  volume = {36},
  number = {1},
  pages = {59--73},
  month = {February},
  year = {2003},
  DOI =  "10.1007/s00453-002-1006-1" 
}

Related publications:

Matthew J. Katz, Frank Nielsen and Michael Segal,
Maintenance of a Piercing Set for Intervals with Applications,
Algorithmica, Springer-Verlag,
Volume 36, pp. 59-73, 2003.
Matthew J. Katz, Frank Nielsen and Michael Segal
Maintenance of a piercing set with applications,
International Symposium on Algorithms and Complexity (ISAAC),
Lecture Notes in Computer Science (LNCS), Springer-Verlag,
Volume 1969, pp. 552-563, 2000.
Matthew J. Katz, Frank Nielsen and Michael Segal,
Shooter Location through Piercing Sets,
Proceedings of the 16th European Workshop on Computational Geometry (CG),
pp. 55-58, 2000.

Last updated, 2003.