Back to my home page.
Constrained Pattern Matching of Point Sets
Frank Nielsen
 Abstract:
Abstract:
Let S={S1, ..., Sn} and Q={Q1, ..., Qm} be two point sets
in the Euclidean d-dimensional space Ed.
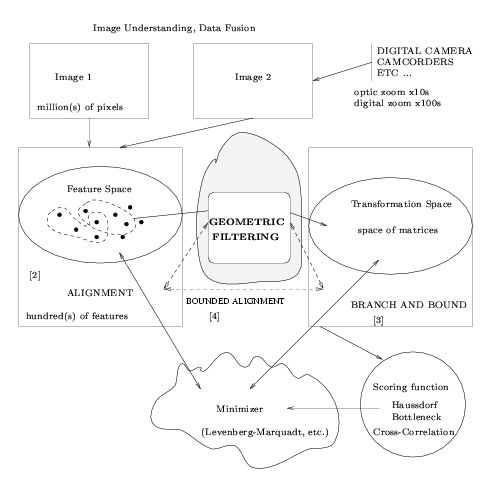
We consider the problem of finding a transformation T of the space of transformations TT so that when applied to point set
S we maximize a matching of {T(S),Q}. We design randomized algorithms that constrain the pattern matching by setting
geometric restrictions on T and extend the approach to geometric hashing.
The time complexity of the algorithms is sensitive to the self-similarity of point sets and relies on the efficiency of
nonlinear range query data-structures.
We present applications of the techniques in vision geometry for image
registrations and its relatives.
Download the PS paper (301 KB size, 3 pages, 1 figure).
Bibtex entry:
@InProceedings{ ak-msrsd-99,
author = {Frank Nielsen},
title = {Constrained Pattern Matching of Point Sets (Extended Abstract)},
booktitle = {Proceedings of the Fifteenth European Workshop on Computational Geometry, Antibes-Juan-les-Pins, France},
pages = {191--193},
year = {1999},
}
Related publications:
Frank Nielsen,
Constrained Pattern Matching of Point Sets,
Proceedings of the 15th European Workshop on Computational Geometry (CG),
pp. 191-193, 1999.
© Copyright notice.
Last updated, 2003.

