Paper: On Piercing Sets of Objects

On Piercing Sets of Objects

Mathhew J. Katz and Frank Nielsen

Abstract:
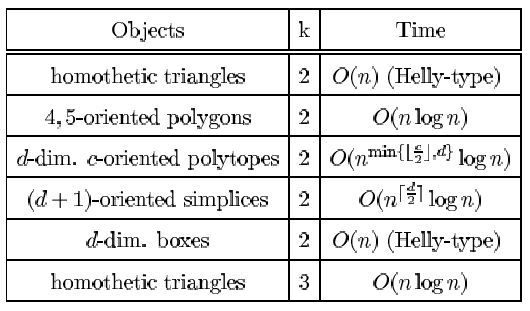
A set of objects is k-pierceable if there exists a set of k points such that each object is pierced by (contains) at least one of these points. Finding the smallest integer k such that a set is k-pierceable is NP-complete. In this paper, we present efficient algorithms for finding a piercing set (i.e., a set of k points a above) for several classes of convex objects and small values of k. In some of the cases, our algorithms imply known as well as new Helly-type theorems, thus adding to previous results of Danzer and Grunbaum who studied the case of axis-parallel boxes. The problems studied here are related to the collection of optimization problems in which one seeks the smallest scaling factor of a centrally symmetric object K, so that a set of points can be covered by k congruent homothets of K

Download the PDF paper (246 Kb size, 15 pages, 2 figures) © ACM Press.

The original publication is available at ACM.

doi: 10.1145/237218.237253

Bibtex entry:

@InProceedings{kn-pso-1996,
    author = "Matthew J. Katz and Frank Nielsen",
    title = "On Piercing Sets of Objects",
    booktitle = "Symposium on Computational Geometry",
    pages = "113-121",
    year = "1996",
    doi ="10.1145/237218.237253"
 }

Related publications:

Matthew J. Katz and Frank Nielsen,
On Piercing Sets of Objects,
ACM Symposium on Computational Geometry (SoCG),
pp. 113-121, 1996.
Matthew J. Katz and Frank Nielsen,
On Piercing Sets of Objects (in PDF),
INRIA RR-2874,
1996.
Frank Nielsen,
On Point Covers of c-Oriented Polygons,
Theoretical Computer Science (Elsevier Computer Science),
Volume 265, Issue 1-2, pp. 17-29, 2001.
Frank Nielsen,
On Point Covering of c-Oriented Polygons,
Canadian Conference on Computational Geometry (CCCG),
pp. 6-7, 1998.
Frank Nielsen,
Fast Stabbing of Boxes in High Dimensions,
Theoretical Computer Science (Elsevier Science),
Volume 246, Issue 1-2, 2000.

Last updated, 2003.