Computational Information Geometry | © Copyright 2007-2014 Frank NIELSEN. All rights reserved
Generalized Bhattacharyya and Chernoff upper bounds on Bayes error using quasi-arithmetic means
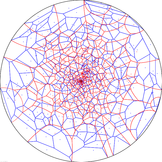(vector graphics HVD.KP.pdf), Hyperbolic Voronoi diagrams (upper space, etc.)
Some R tutorial/code for computing the Jeffreys centroid (symmetric Kullback-Leibler divergence, SKL).
This web site is currently heading for a renewal. Stay tuned...

Computational Information Geometry

Computational information geometry deals with the study and design of efficient algorithms in information spaces using the language of geometry (such as invariance, distance, projection, ball, etc). Historically, the field was pioneered by C.R. Rao in 1945 who proposed to use the Fisher information metric as the Riemannian metric. This seminal work gave birth to the geometrization of statistics (eg, statistical curvature and second-order efficiency). In statistics, invariance (by non-singular 1-to-1 reparametrization and sufficient statistics) yield the class of f-divergences, including the celebrated Kullback-Leibler divergence. The differential geometry of f-divergences can be analyzed using dual alpha-connections. Common algorithms in machine learning (such as clustering, expectation-maximization, statistical estimating, regression, independent component analysis, boosting, etc) can be revisited and further explored using those concepts. Nowadays, the framework of computational information geometry opens up novel horizons in music, multimedia, radar, and finance/economy.  
 
Participate to the Léon Brillouin seminar on information geometry sciences !
 
Subscribe to the infogeo mailing-list for announcements (conferences, libraries, positions, etc)
 
What is new?
Online dictionary of distances, measures and means (registration required)
*** To open in August/September 2011 ***
 
Visit the blog or twitter threads FrnkNlsn
Consider taking the quizzs: quizz 1 quizz 2 quizz 3 quizz 4
R.A. Fisher Digital Archive
private area
The field of computational information geometry (discrete information geometry) is interested in exploring the following domains:
Let us give some examples of information manifolds: Strictly speaking, geometrizing information-theoretic problems does not provide a more powerful framework in theory. This is because synthetical and analytical geometries are equivalent. Informally, that means that we can do geometry by algebraic equations. However, geometrizing problems help grab intuition on the problem at hand. Geometry also yields novel notions to mathematical theories. For example, let us cite the two curvature notions in statistics: exponential and mixture curvatures emanating from conjugate connections. So although synthetical geometry provides the same power as analytical geometry, the third-order asymptotic theory of statistics has been obtained so far only from synthetical information geometry. Dual differential geometries are also useful to tackle information-theoretic problems such as

Publications

Journals

Conferences

Software

  • Maximum Entropy Modeling Toolkit for Python and C++
    International Workshop on Matrices and Statistics (with historical note Computational information geometry: Pursuing the meaning of distances
    Online December 2007. Last updated, January 2011.
    © 2007-2011 Frank NIELSEN, All rights reserved.